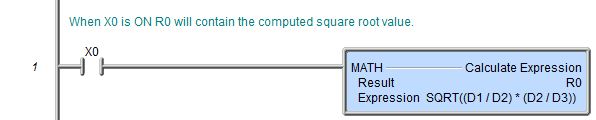
Topic: DMD0085

Help File Version: 2.10.0.636

MATH - Calculate Expression

The Calculate Expression (MATH) instruction is used to perform complex mathematical calculations, using a format similar to that used in a spreadsheet or common programming languages. Each expression can be nested or chained to generate simple to complex expressions. Parentheses can be nested up to 8 levels deep.

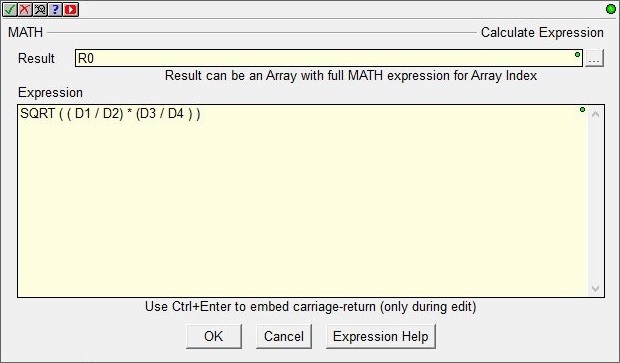
After entering the contents of the expression, click OK to save the contents and close the editor, click Cancel to close the editor without saving the changes, or click Expression Help to open the Help topic for all of the math operators and functions that can be used in an expression.

C/C++ rules (not PEMDAS) are used to solve the math expression. Liberal use of parentheses to remove any ambiguity in the processing order is encouraged.

The precedence rule order used is as follows:

Unary Operator Group (-)

Exponential Group (**)

Multiply Group (* / %)

Add Group (+ -)

Shift Op Group (<< >> >>>)

Inequality Group (< > <= >=)

Equality Group (== !=)

& (Bit-wise AND)

^ (Bit-wise XOR)

| (Bit-wise OR)

&& (logical AND)

|| (logical OR)

Note: parentheses will be added by the editor when saving mixed-operator math expressions. If the expression that is saved by the editor is NOT what is expected, reopen the editor and manually add the parentheses required to get the desired expression.

Math Promotion / Demotion

The Do-more CPU is natively a 32-bit processor. Although many different data formats and sizes are supported, whenever an instruction must do a calculation with a PLC element that is NOT a 32-bit value, that value gets " promoted". This means that whenever elements that are UNSIGNED BYTE, SIGNED BYTE, UNSIGNED WORD, or SIGNED WORD are used in a math calculation, they are processed natively as 32 bit signed integer. All of these data types easily fit and all of their values are supported as native 32 bit signed integers.

Most mathematical calculations that take integers for their inputs will also return an integer. For example, when dividing two integers, the CPU performs integer division, not floating point division, meaning that integer 5 divided by integer 2 is integer 2, not the Real value 2.5.

However, if a real value is ever part of a mathematical calculation, as soon as the real value is introduced into the calculation, the math processor starts performing floating point calculations on ALL operations going forward. This will include automatically promoting any intermediate integer values to their floating point equivalent. For example, the equation (5 + 2) / 2.0 will calculate 5 + 2 as integer and the intermediate result will be integer 7, but when the integer 7 is divided by the floating point value 2.0, the math processor performs a floating point divide operation, which will promote the integer 7 to 7.0, and the result will be the real value of 3.5.

There is an exception to this rule that involves the math calculation processing a math function that returns an integer value, like TRUNC() or ROUND(). If the math processor was processing real operations, then processing any of the math functions that return an integer will return the math processor to using integer math going forward.

The most common mistake occurs when dividing two integer values but the desired result is a fractional real result. Use the TOREAL() function to promote an integer value or integer expression to its real equivalent. For example, if you want to divide D10 by D11, and get a fractional floating point result, either of the following will give the desired result:

• TOREAL(D10) / D11
   

• D10 / TOREAL(D11)
   

• TOREAL(D10) / TOREAL(D11)

The thing to remember is that when a calculation involves both integer and floating point types, the integer types will be automatically promoted to floating point values so that the calculation can be performed using all floating point types. Floating point types are automatically truncated to integers when the program expects an integer value, for example, when a floating point variable is assigned to an integer variable.

When assigning an integer or real value to a Bit element, integer and real values of zero / non-zero are evaluated as OFF / ON for the Bit.

All error conditions that arise while calculating an expression will be reported on the System Status page of the System Information dialog, and an appropriate system-level Bit location ($IndexError, $OutOfRange, $Overflow, $DivedByZero, etc.) will also be set ON.

Math Execution Speed

Integer math is FAST, and Integer math is ACCURATE. Do-more CPUs have 32 bits of integer accuracy, which is +/- 2 billion. If a million BYTE values of 255 are added together and the result (255,000,000 will fit in a 32-bit D location.

Floating point math is SLOWER (not SLOW, just SLOWER). It has 24 bits of ”accuracy” (7 bits for exponent, 1 bit for sign, for all 32 bits). For example, an attempt to add 1,000,000 (one million) to .0000001 (one millionth), will not result in 1,000,000.0000001, because a single REAL cannot hold THAT much accuracy in 32 bits. Real locations have the ability to store a large range of possible values within one 32 bit register, from very small to very large numbers (e.g. 0.0000001 and 1,000,000 or even 6.02 x 1023). There is a loss of accuracy, e.g. you cannot store EXACTLY 3.3, and you can’t add really large and really small numbers together and retain all of the accuracy of both numbers.

A single MATH box allows the programmer to freely mix REAL and integers, so the questions arise: when is accuracy lost? When is speed lost?

The Do-more CPU will attempt to use integer math for all computations because it is fast and accurate. But when a REAL value is introduced, from that point forward, the remaining calculations will all be done in REAL. This is a bit of an oversimplification, because, when you have sub-expressions, each sub-expression obeys this rule, not just left-to-right at the ASCII expression level).

Here's an example: the calculation (CT0.Acc + CT1.Acc + CT2.Acc) / 3 is performed using all integer math. The calculation result is integer. Integer division is one case where you do lose accuracy; it TRUNCATES. 1 / 3 is 0. 2 / 3 is 0. 3 / 3 is 1. 4 / 3 is 1. However, remember that the calculation will start using FLOATING POINT MATH for all subsequent calculations once it is introduced.

If the alter the calculation to (CT0.Acc + CT1.Acc + CT2.Acc) / 3.0, Integer math is used on the on the 3 counter accumulators in the numerator (which is great for speed and accuracy), but the division is done with the REAL value 3.0, not the INTEGER value 3.

When the division is done with a REAL the calculation is performed as a floating point operation. This will produce the desired result as long as that result is stored in a REAL memory location.

What if the denominator is a non-REAL memory location, like V? For example: (CT0.Acc + CT1.Acc + CT2.Acc) / V10. Since V memory locations contain integer values, and the desired result is a REAL, the value in the V location must be converted to REAL value. Note: in this case do not use casts, for example: do not use V10:R. Casting is for reinterpreting the bit pattern, not for data conversions.

The MATH function called TOREAL() will perform the needed conversion. It takes the expression that is in parentheses and converts it TO REAL. If the expression is an integer, it converts it to a REAL. If the expression is already a REAL value, it doesn’t do anything.

If V10 contains the integer value 3 then (CT0.Acc + CT1.Acc + CT2.Acc) / TOREAL(V10) would generate the desired result.

Alternatively, TOREAL(CT0.Acc + CT1.Acc + CT2.Acc) / V10 would give the same result, but floating point calculations would be performed for the entire calculation instead of just the division.

The rule of thumb is to do integer math as long as possible when you know you will not lose accuracy. Addition and subtraction are always good for integers. Multiplication and division are usually good with integers, but multiplying two large 32 bit numbers that will exceed 32 bits won’t work, the multiplication must be done as floating point. Division is good with integers when decimal point accuracy is not needed.

Parameters:

Note: Use the F9 key or click the 'three dot box' at the right edge of the parameter field to open the Default Element Selection Tool (the Element Picker or the Element Browser) or use the Down-Arrow key (Auto-Complete) on any parameter field to see a complete list of the memory locations that are valid for that parameter of the instruction.

Result is a location to store the result of the math computation. This can be any writable numeric location or an array reference.

Note: as of Do-more Technology Version 1.4, if the result is an array reference, the array index can be a full expression, e.g. D[V10 +32] .

Expression contains the memory locations, mathematical operators, and / or math functions from the following tables that make up the formula to calculate. This can be any valid combination of constant values, bit or numeric memory locations, math operators, nested parentheses, and math functions up to a maximum of 1024 characters. Expressions can be nested up to 8 levels deep and chained between operators within function parameters, and as array indices, so use of parentheses is recommended to ensure proper evaluation order.

Rung Example: